English language Spanish language  Portuguese language 
You are here : > Home> Utilities> Geometry > Hyperbola >



Hyperbola


Hyperbola is a conic section in which the distances of all points on the curve, from the focus, are proportional to the distances from the focus to the line called the directrix.
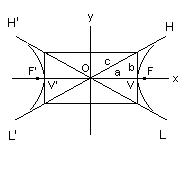
Hyperbole has two branches, which can be oriented either in the direction of the transverse axis or the conjugate..
The standard equation of the hyperbola with center at the origin of the Cartesian axes is:
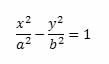
Hyperbola


Thus, we have: a = √a2  and   b = √b2
The elements of the hyperbola are calculated in this application in accordance with the standard equation, shown above, in which a> b. When the center of the hyperbola is outside of the center of Cartesian axes, enter the coordinates "X0" and "Y0".
Enter data using the point as a decimal separator. Ex: 1370.34; the results will be shown after a click on Calculate.

Hyperbola

Them a = √a2;
Hyperbola
Decimal places:
a(real semi-axis) :
b:(imaginary semi-axis):
Center (X0):
Center (Y0):
     
Focus F':
Focus F:
Vertex V':
Vertex V:
Directrices:
Focal distance:
Focal parameter:
Transverse axis(x):
Conjugate axis(y):
Eccentricity:
Asymptote H' L:
Asymptote L' H:

Note:The accuracy of the calculator and its applicability to particular cases is not guaranteed.






Related Topics

Right Triangle Isosceles Triangle Equilateral Triangle Scalene Triangle Square Rectangle Trapezium Right-Angled Trapezoid Isosceles Trapezoid Rhombus Regular polygon Polygon names Circle Pyramid Triangle pyramid Square pyramid Rectangular pyramid Cube Prism Rectangle Prism Cone Cylinder Sphere Ellipse Parabola Hyperbola